实验报告
姓名 王煜
班级 18物联
实验时间 5.16
实验地点 514教室
6.4.1
实验一
1、实验目的
调用area()函数求三角形的面积
在求面积函数中运用海伦公式
2、问题描述
编写程序,从键盘输入三角形三边,调用三角形面积函数求其面积,并输出结果。
3、流程图
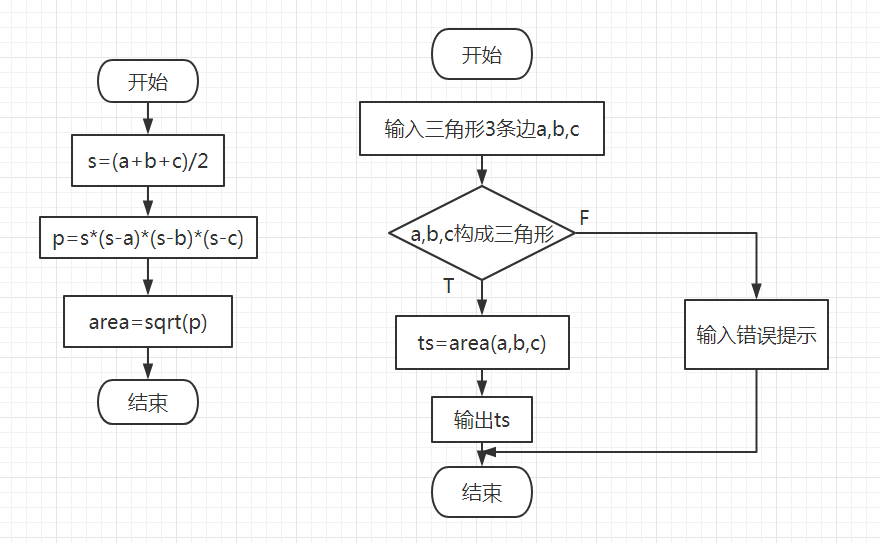
4、实验代码
#include#include float area(float a,float b,float c){ float s,p,area; s=(a+b+c)*0.5; p=s*(s-a)*(s-b)*(s-c); area=sqrt(p);/*海伦公式求三角形面积*/ return (area);}main(){ float x,y,z,ts; scanf("%f%f%f",&x,&y,&z);/*输入三边*/ ts=area(x,y,z);/*三角形面积函数*/ if(x+y>z&&x+z>y&&z+y>x)/*判断是否构成三角形*/ printf("area=%f\n",ts); else printf("data error!"); }
5、输出结果
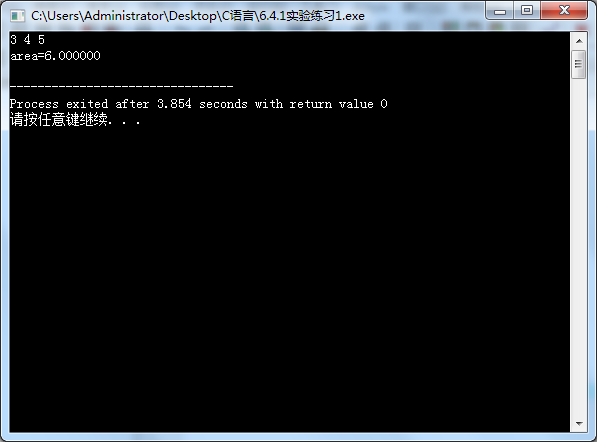
6.4.1实验二
1、实验目的
定义符号常量
使用长整型变量存放累乘积
在函数中,使用局部静态变量存放累乘积
使用全局变量存放累乘积
2、问题描述
编写函数,求出主调函数传来的数值i的阶乘值,然后将其传回主调函数并输出。
3、流程图
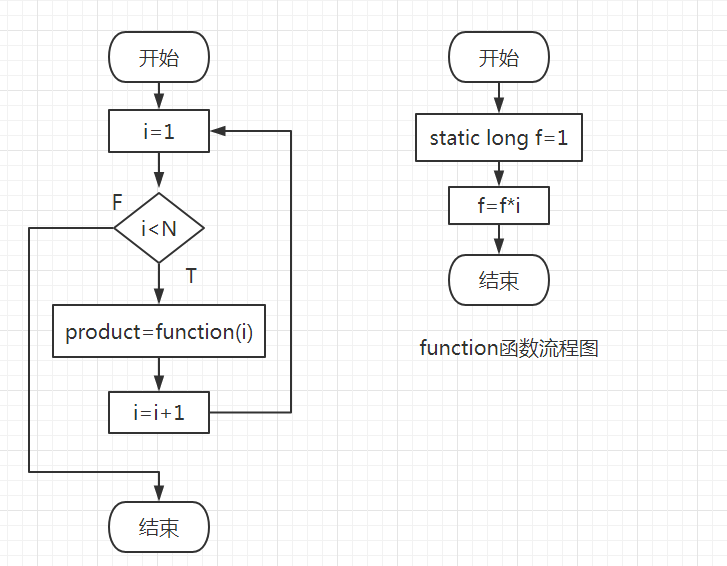
4、实验代码
#includeint fac(int n){ static int f=1; f=f*n; return f;}main(){ int i,x,jc; scanf("%d",&x); for(i=1;i<=x;i++) { jc=fac(i); printf("%d的阶乘值为:%d\n",i,jc); }}
5、输出结果
6.4.1实验三
1、实验目的
调用gcd()函数求两个整数的最大公约数
掌握辗转相除法求两个整数的最大公约数
2、问题描述
编写程序,从键盘输入两个整数,调用gcd()函数求他们的最大公约数,并输出结果。
3、流程图
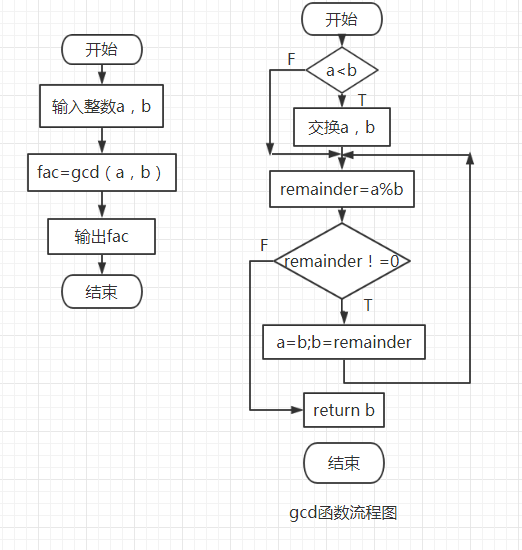
4、实验代码
#includemain(){ int x,y; scanf("%d%d",&x,&y); int t=x; if(t>y) t=y; for(int i=t;i>=1;i--) { if(x%i==0&&y%i==0) { printf("最大公约数是%d\n",i); break; } }}
5、输出结果
6.4.1实验四
1、实验目的
调用trangle()函数输出三角形
在trangle()函数中用for循环的嵌套输出指定的结果
2、问题描述
输入整数n,输出高度为n的等边三角形。
3、流程图
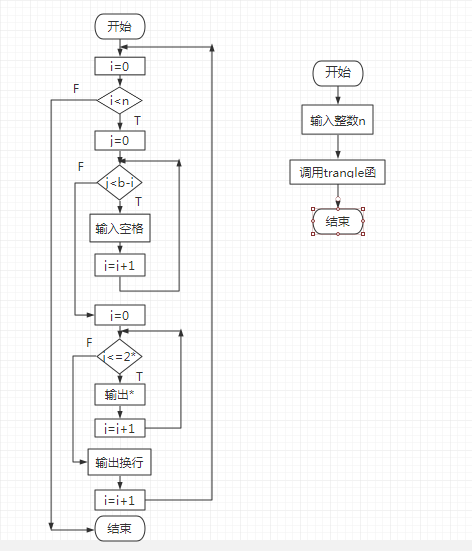
4、实验代码
#includevoid trangle(int n){ int i,j; for(i=0;i
5、输出结果
6.4.2实验一
1、实验目的
掌握C语言中定义函数的方法
掌握通过“值传递”调用函数的方法
2、问题描述
求500以内的所有亲密数对
3、流程图
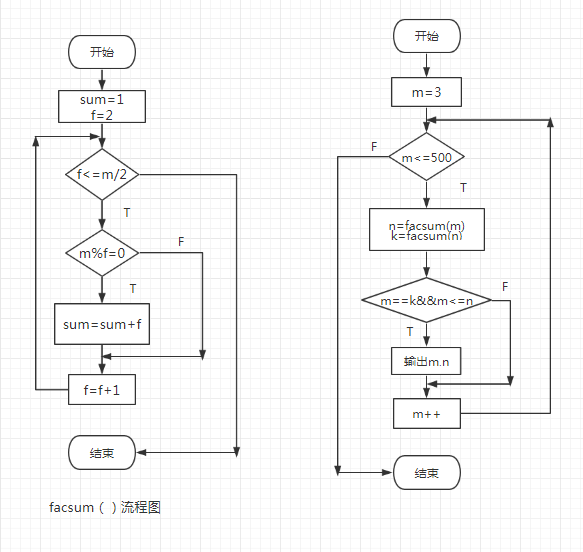
4、实验代码
#includeint facsum(int m){ int sum=1,f=2; while(f<=m*0.5) { if(m%f==0) { sum=sum+f; } f++; } return sum;}main(){ int m=3,n,k; while(m<=500) { n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf("%d,%d\n",m,n); m++; }}
5、输出结果

6.4.2实验二
1、实验目的
掌握C语言中定义函数的方法
掌握通过“值传递”调用函数的方法
2、问题描述
(1)编制一个函数sab(a,b,n),其功能为利用复化梯形公式计算定积分s=fa~bf(x)dx其中n为对区间【 a,b】的等分数。要求在一个独立的文件中。
(2)编制一个主函数以及计算被积函数值的函数f(x),在主函数中调用(1)中的函数sab(a,b,n)计算并输入下列积分值s=0~1 e的x次方dx,取n=10,要求在一个独立的文件中。
(3)编制另一个主函数以及计算被积分函数值的函数f(x),在主函数中调用(1)中的函数sab(a,b,n)计算并输出下列积分值s=-1~1 1/(1+25x*x)dx,取n=8。要求在一个独立的文件中
3、流程图
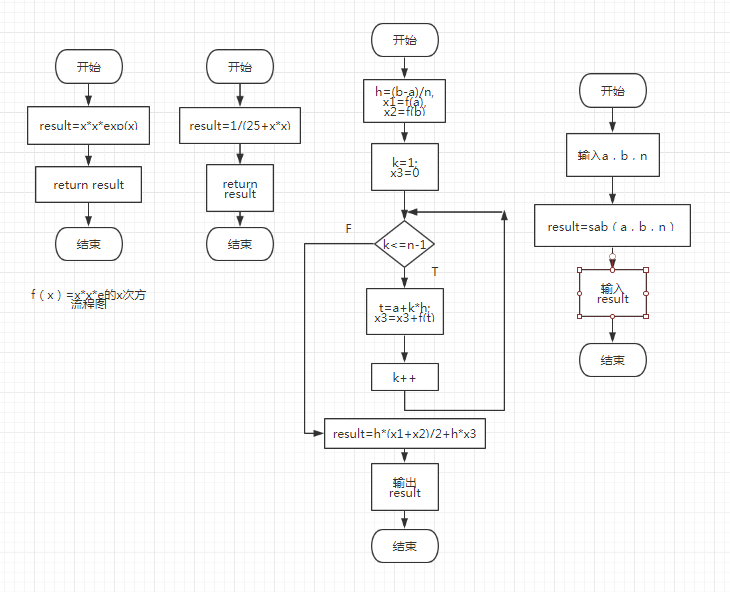
4、实验代码
#includedouble f(double x);double sab(double a,double b,int n){ double h,result,x1,x2,x3=0,t; int k; h=(b-a)/n; x1=f(a); x2=f(b); for(k=1;k<=(n-1);k++) { t=a+k*h; x3=x3+f(t); } result=h*(x1+x2)*0.5+h*x3; return result;}
#include#include #include"sab.h"double f(double x){ double result; result=x*x*exp(x); return result;}main(){ double a,b,result; int n; printf("plz enter abn:"); scanf("%lf%lf%d",&a,&b,&n); result=sab(a,b,n); printf("sab(%lf,%lf,%d)=%lf",a,b,n,result); return 0;}
#include#include"sab.h"double f(double x){ double result; result=1/(25+x*x); return result;}main(){ double a,b,result; int n; printf("plz enter abn:"); scanf("%lf%lf%d",&a,&b,&n); result=sab(a,b,n); printf("sab(%lf,%lf,%d)=%lf",a,b,n,result); return 0;}
5、输出结果
6.4.2实验三(不懂不懂)
1、实验目的
掌握递归函数的设计方法
进一步练习阅读检查与调试修改C程序的方法
2、问题描述
(1)编制计算Ackerman函数的递归函数ack(n,x,y)
(2)编制一个主函数,由键盘输入n,x,y,调用(1)中的函数ack(n,x,y),计算Ackerman函数
(3)在主函数中,输入之前要有提示,并检查输入数据的合理性,若输入的数据不合理,则输出出错信息。
(4)输入(n,x,y)=(2,3,1)运行该程序。然后自定义几组数据再运行该程序。
Ackerman函数定义如下:n,x,y为非负整数,且
ack(n,x,y)=x+1 n=0
x n=1且y=0
0 n=2且y=0
1 n=3且y=0
2 n>=4且y=0
ack(n-1, ack(n,x,y-1), x) n!=0且y!=0
3、流程图
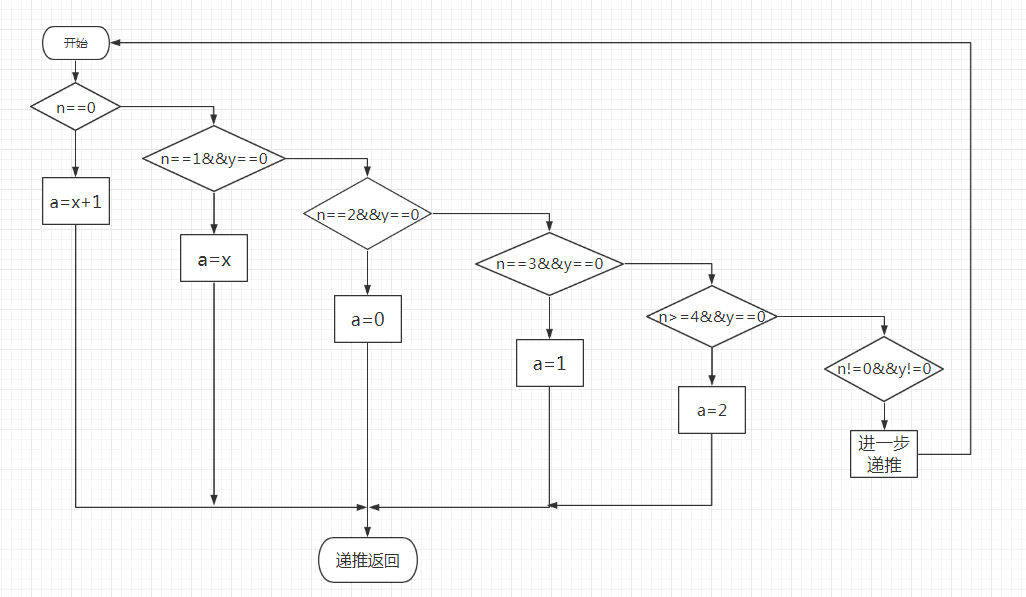
4、实验代码
#includeint ack(int n,int x,int y){ int a; if(n==0) a=x+1; if(n==1&&y==0) a=x; if(n==2&&y==0) a=0; if(n==3&&y==0) a=1; if(n>=4&&y==0) a=2; if(n!=0&&y!=0) a=ack(n-1,ack(n,x,y-1),x); return a;}main(){ int n,x,y,result; printf("plz enter nxy:"); scanf("%d%d%d",&n,&x,&y); if(n<0||x<0||y<0) { printf("sorry U enter a erorr number,plz enter a new number"); scanf("%d%d%d",&n,&x,&y); } result=ack(n,x,y); printf("Ack(%d,%d,%d)=%d",n,x,y,result);}
5、输出结果

6.4.3实验一
1、实验目的
写出解决该问题的递归算法 getpower(x,y)=x y=1
x*getpower(x,y-1) y>=2
在递归函数中,使用数字数字1作为回归条件
在递归函数中,使用if_else语句根据条件的真假来决定是递归还是回归
2、问题描述
编写程序,分别从键盘输入数据x和y,计算x的y次幂并输出。
3、流程图
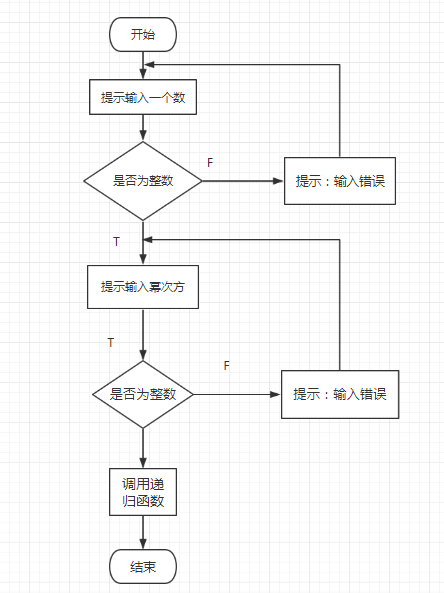
4、实验代码
#includelong getpower(int x,int y){ if(y==1)/*判断回归条件的if语句头部*/ return x; else return x*getpower(x,y-1);/*进一步递推的语句*/}main(){ int num,power; long answer; printf("输入一个整数:");/*提示输入一个数*/ scanf("%d",&num);/*输入一个整数*/ printf("输入幂次方:");/*提示输入幂次方*/ scanf("%d",&power);/*输入一个整数*/ answer=getpower(num,power);/*用输入的数,调用递归函数*/ printf("结果是:%ld\n",answer);}
5、输出结果
6.4.3实验二
1、实验目的
写出解决该问题的递归算法
在递归函数中1,使用数字1作为回归条件
在递归函数中,使用if_else语句根据条件的真假来决定是递推还是回归
2、问题描述
哟吗递归方法计算学生的年龄。已知第一个学生的年龄最小为10岁,其余学生一个比一个大2岁,求第5位学生的年龄。
3、流程图
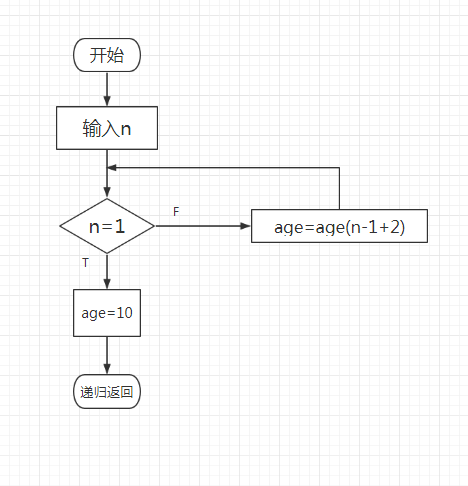
4、实验代码
#includeint age(int n){ int c; if(n==1)/*判断回归条件的if语句头部*/ c=10; else return age(n-1)+2;/*进一步递推的语句*/ return c;}main(){ int n=5; printf("第%d位学生的年龄为%d",n,age(n));/*调用递归函数输出第五位学生的年龄*/}
5、输出结果
6.4.3实验三
1、实验目的
根据递归公式编写递归函数
在递归函数中,使用if_else语句根据条件的真假来决定是递推还是回归
2、问题描述
问题的简单描述:定义递归函数实现下列Ackman函数:Acm(m,n)=n+1 (m=0)
Acm(m-1,1) (n=0)
Acm(m-1, Acm(m,n-1)) (n>0,m>0)
3、流程图
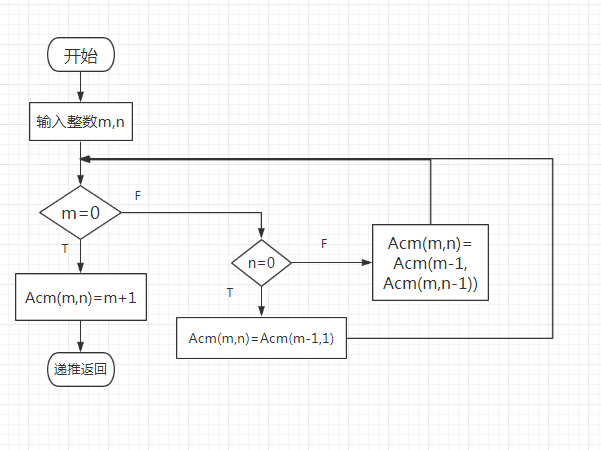
4、实验代码
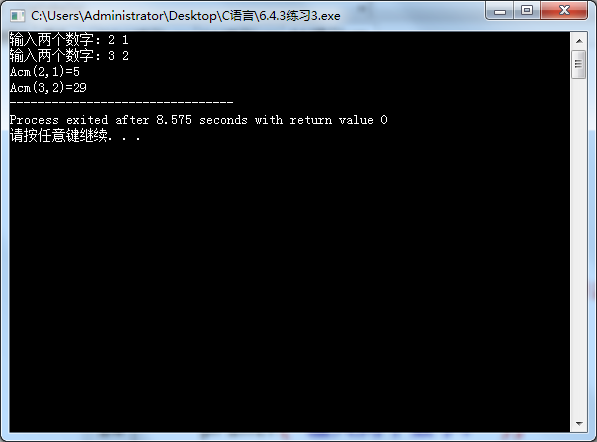
#includeAcm(int m,int n){ if(m==0) return n+1; if(n==0) return Acm(m-1,1); if(n>0&&m>0) return Acm(m-1,Acm(m,n-1));/*进一步递推的语句*/ }int main(){ int m,n,x,y; printf("输入两个数字:"); scanf("%d%d",&m,&n);/*调用Acm函数输出Acm(2,1)和Acm(3,2)的结果*/ printf("输入两个数字:"); scanf("%d%d",&x,&y); printf("Acm(%d,%d)=%d\nAcm(%d,%d)=%d",m,n,Acm(m,n),x,y,Acm(x,y)); return 0;}
5、输出结果